Declinining balance depreciation and salvage value

[Clement]

Hi,

When depreciating an asset with the declining balance method, what happens if at the end of the useful life of the asset, the book value of the asset is higher than the salvage value of the asset?
On one hand, the depreciation should stop since the useful life is over.
On the other hand, the depreciation should continue since the salvage value hasn't been reached yet.

Am I missing something?

 

[kirby]

Adjust the book value down to the salvage value.

 

[Clement]

That could be a big amount potentially though.
I read recently somewhere that once straight line depreciation is higher than declining balance then switch to straight line, which would mean that salvage value always get reach at end of life.

 

[WeirdVibeInc]

I was wondering about this too. Curving down with DB or DDB goes faster than SL at first, but then crosses the SL plot. The limit of the DB/DDB curve is always higher than the salvage value. So at end-of-life, there's a giant step down.

It seems like the method that would actually be wanted would be an exponential decay curve that has a limit at the salvage value, e.g.:

y = ( (original value - salvage value) * e ^ -(Mx) ) + salvage value

...where M is a modifier to adjust the curve to come down near the limit at about the end of its life. For 5 years, it seems like M=0.8 looks like a good value.

Try it on a graphing calculator: https://www.desmos.com/calculator

For example, if my original value is $100, salvage value is $20 or 20%, and lifespan is 5 years, M=0.8 gives a good curve:

 

[WeirdVibeInc]

Incidentally, this study seems helpful -- with regard to technology, actual value doesn't follow DDB, but that's what rules allow. So the rules are wrong and accountancy needs to catch up to reality... but the actual curve isn't a simple exponential decay either.

"Under current tax rules (the “Modified Accelerated Cost Recovery System”), PCs and other types of computing equipment are depreciated over a five-year period. The annual deductions are calculated using the “double-declining-balance” (DDB) method with a switch to the straight-line method at the point that maximizes the present value of the deductions. The double-declining-balance method specifies an annual percentage deduction that is twice the straight-line rate. For an asset with a five-year recovery period, the DDB deduction rate would be 40 percent annually."

https://www.federalreserve.gov/pubs/feds/2004/200431/200431pap.pdf

But that statement doesn't take into account that the straight line deduction rate is determined by the difference between the purchase value and the approximated salvage value of the individual asset divided by the number of years of useful life, which could be something other than 20%. For example, you could probably resell a Windows 10 rendering platform as a gaming machine or refurbished with Linux for a higher percentage of the purchase price than you could an iPad that can't be updated anymore.

 

[DrStrangeLove]

That could be a big amount potentially though.
I read recently somewhere that once straight line depreciation is higher than declining balance then switch to straight line, which would mean that salvage value always get reach at end of life.

Every depreciation method eventually gets to the salvage value; they only differ in the path they take to get there.

The argument to adjust the book value down to salvage value is analogous to recoverability/impairment. At the end of its useful life the asset can only be realized for its salvage value. The conservatism in GAAP requires that the asset not be valued for more than its realizable value.

To put it another way: to the extent that depreciation is about recovering cost, once the asset reaches the end of its useful life, the owner has recovered all the depreciable value (cost) it can. The only remaining amount that can be realized from the asset is its salvage value.

 

[WeirdVibeInc]

Every depreciation method eventually gets to the salvage value; they only differ in the path they take to get there.

To put it another way: to the extent that depreciation is about recovering cost, once the asset reaches the end of its useful life, the owner has recovered all the depreciable value (cost) it can. The only remaining amount that can be realized from the asset is its salvage value.

What are the actual formulas for SL, DB, and DDB? I've seen it a bunch of different ways in various blogs and financial magazine sites. Nothing but SL ever seems to make sense.

 

[DrStrangeLove]

What are the actual formulas for SL, DB, and DDB? I've seen it a bunch of different ways in various blogs and financial magazine sites. Nothing but SL ever seems to make sense.

Closed-form formulas aren't as important as understanding the process for calculating the depreciation expense for each year. (This is why we have calculators and spreadsheets.)

Straight-line is obvious. The depreciable amount is cost less salvage value. If an asset's useful life is n years, depreciation expense is 1/n * (cost less salvage value) per year for n years. Easy peasy. Simple linear function; same amount of depreciation each year.

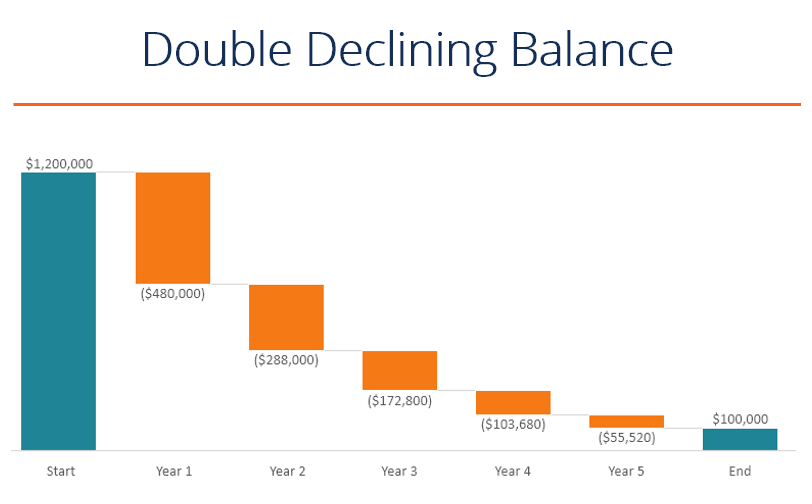
Double declining balance: Start with the same depreciable amount. If the useful life is again n years, you depreciate 2/n of the remaining depreciable amount each year, with a floor at zero. So the depreciable amount left after k years will be initial depreciable amount * (1 - 2/n)^k, where k = 1, 2,..., n - 1. Year n's depreciation expense is whatever depreciable value is left at the end of year n -1/start of year n, since that's the end of the asset's useful life. Not as easy, and a bit less peasy. The rate of depreciation is constant (up till the final year), but the amount of depreciation declines each year as the depreciable amount amortizes. The link below has a really clear example that walks you through the calculation, if that helps.

And 100k% declining balance is a generalization of double declining balance. The depreciation rate is k/n instead of 2/n, but the algorithm is otherwise the same.

Double Declining Balance Depreciation Template

This double declining balance depreciation template will help you find depreciation expense using one of the most common depreciation methods.

corporatefinanceinstitute.com